Una tensostruttura è una costruzione di elementi che trasportano solo tensione e nessuna compressione o flessione .
Il termine trazione non deve essere confuso con tensegrità , che è una forma strutturale con elementi sia di trazione che di compressione. Le tensostrutture sono il tipo più comune di strutture a guscio sottile .
Tensegrità è un termine coniato dall’ingegnere Richard Buckminster Fuller per indicare un insieme di «tensione» e «integrità» (o coesione). Si tratta di una proprietà attribuita agli oggetti i cui componenti usano trazione e compressione in modo combinato, al fine di fornire loro stabilità e resistenza.
La maggior parte delle tensostrutture sono supportate da una qualche forma di elementi di compressione o flessione, come alberi (come in The O 2 , ex Millennium Dome ), anelli di compressione o travi.
Una struttura a membrana in tensione viene spesso utilizzata come tetto , in quanto può coprire grandi distanze in modo economico e attraente. Le strutture a membrana di tensione possono anche essere utilizzate come edifici completi, con alcune applicazioni comuni come impianti sportivi, edifici di deposito e stoccaggio e sedi espositive.
Questa forma di costruzione è divenuta più rigorosamente analizzata e diffusa nelle grandi strutture solo nell’ultima parte del XX secolo. Le tensostrutture sono state a lungo utilizzate nelle tende , dove i tiranti e i pali della tenda forniscono pretensionamento al tessuto e gli consentono di resistere ai carichi.
L’ingegnere russo Vladimir Shukhov è stato uno dei primi a sviluppare calcoli pratici di sollecitazioni e deformazioni di tensostrutture, gusci e membrane. Shukhov ha progettato otto padiglioni espositivi per tensostrutture e strutture a guscio sottile per la fiera di Nizhny Novgorod del 1896 , coprendo un’area di 27.000 metri quadrati. Un uso più recente su larga scala di una tensostruttura rivestita di membrana è il Sidney Myer Music Bowl , costruito nel 1958.
Antonio Gaudi ha utilizzato il concetto al contrario per creare una struttura di sola compressione per la chiesa di Colonia Guell . Ha creato un modello di trazione sospesa della chiesa per calcolare le forze di compressione e per determinare sperimentalmente le geometrie della colonna e della volta.
L’ Olympiastadion di Monaco fa ampio uso di tensostrutture per tetti.
Il concetto è stato successivamente sostenuto dall’architetto e ingegnere tedesco Frei Otto , il cui primo utilizzo dell’idea è stato nella costruzione del padiglione della Germania occidentale all’Expo 67 di Montreal. Otto utilizzò successivamente l’idea per il tetto dello Stadio Olimpico per le Olimpiadi estive del 1972 a Monaco .
Dagli anni ’60, le tensostrutture sono state promosse da designer e ingegneri come Ove Arup , Buro Happold , Walter Bird of Birdair, Inc. , Frei Otto , Mahmoud Bodo Rasch , Eero Saarinen , Horst Berger , Matthew Nowicki , Jörg Schlaich , il duo di Nicholas Goldsmith e Todd Dalland presso FTL Design & Engineering Studio e David Geiger .
Il costante progresso tecnologico ha aumentato la popolarità delle strutture con tetto in tessuto. Il peso ridotto dei materiali rende la costruzione più semplice ed economica rispetto ai progetti standard, soprattutto quando è necessario coprire ampi spazi aperti.
Tipi di struttura con membri di tensione significativi
Strutture lineari
- Ponti sospesi
- Cavi drappeggiati
- Strallato travi o capriate
- Tralicci per cavi
- Cavi tesi diritti
Strutture tridimensionali
- Ruota di bicicletta (può essere utilizzata come tetto in orientamento orizzontale)
- Tralicci 3D
- Strutture di tensegrità
Strutture sottoposte a sollecitazioni superficiali
- Membrane precompresse
- Membrane sollecitate pneumaticamente
- Gridshell
- Struttura in tessuto
Strutture di cavi e membrane
Materiali a membrana
I materiali comuni per le strutture in tessuto a doppia curvatura sono fibra di vetro rivestita in PTFE e poliestere rivestito in PVC . Si tratta di materiali intrecciati con diversi punti di forza in diverse direzioni. Le fibre di ordito (quelle fibre che sono originariamente diritte, equivalenti alle fibre di partenza su un telaio) possono sopportare un carico maggiore rispetto alle fibre di trama o di riempimento, che sono intessute tra le fibre di ordito.
Altre strutture fanno uso di film di ETFE , sia come strato singolo che sotto forma di cuscino (che può essere gonfiato, per fornire buone proprietà di isolamento o per effetto estetico, come nell’Allianz Arena di Monaco ). I cuscini in ETFE possono anche essere incisi con motivi per far passare diversi livelli di luce quando gonfiati a diversi livelli.
Alla luce del giorno, la traslucenza della membrana in tessuto offre spazi morbidi e diffusi con luce naturale, mentre di notte l’illuminazione artificiale può essere utilizzata per creare una luminescenza esterna ambientale. Sono molto spesso supportati da un telaio strutturale in quanto non possono trarre la loro forza dalla doppia curvatura.
Cavi
I cavi possono essere in acciaio dolce , acciaio ad alta resistenza (acciaio al carbonio trafilato), acciaio inossidabile , fibre di poliestere o aramidiche . I cavi strutturali sono costituiti da una serie di piccoli trefoli attorcigliati o legati insieme per formare un cavo molto più grande. I cavi di acciaio sono o trefoli a spirale, in cui le aste circolari vengono attorcigliate e “incollate” utilizzando un polimero, o un trefolo a spirale bloccato, dove i singoli trefoli di acciaio ad incastro formano il cavo (spesso con un nucleo a spirale).
Il filo a spirale è leggermente più debole del filo a spirale bloccato. I cavi a spirale in acciaio hanno un modulo di Young , E di 150 ± 10 kN / mm² (o 150 ± 10 GPa ) e sono disponibili in dimensioni da 3 a 90 mm di diametro.
Il trefolo a spirale soffre di allungamento della costruzione, dove i trefoli si compattano quando il cavo viene caricato. Questo viene normalmente rimosso prestando il cavo e facendo salire e scendere il carico fino al 45% del carico di trazione finale.
Il filo della bobina bloccato ha tipicamente un modulo di Young di 160 ± 10 kN / mm² ed è disponibile in dimensioni da 20 mm a 160 mm di diametro.
Le proprietà dei singoli trefoli di materiali diversi sono mostrate nella tabella seguente, dove UTS è la resistenza a trazione ultima o il carico di rottura:
| E (GPa) | UTS (MPa) | Filtrare al 50% di UTS | |
|---|---|---|---|
| Barra d’acciaio solida | 210 | 400–800 | 0,24% |
| Filo d’acciaio | 170 | 1550–1770 | 1% |
| Fune | 112 | 1550–1770 | 1,5% |
| Fibra di poliestere | 7.5 | 910 | 6% |
| Fibra aramidica | 112 | 2800 | 2,5% |
Forme strutturali
Le strutture ad aria sono una forma di tensostrutture in cui l’involucro in tessuto è supportato solo da aria pressurizzata.
La maggior parte delle strutture in tessuto trae la sua forza dalla forma doppiamente curva. Costringendo il tessuto ad assumere una doppia curvatura, il tessuto acquisisce una rigidità sufficiente per resistere ai carichi a cui è sottoposto (ad esempio vento e carichi di neve ). Per indurre una forma adeguatamente doppiamente curva è molto spesso necessario pretensionare o precomprimere il tessuto o la sua struttura portante.
Ricerca di moduli
Il comportamento delle strutture che dipendono dalla precompressione per raggiungere la loro resistenza non è lineare, quindi qualsiasi cosa diversa da un cavo molto semplice è stata, fino agli anni ’90, molto difficile da progettare. Il modo più comune per progettare strutture in tessuto doppiamente curve era costruire modelli in scala degli edifici finali al fine di comprenderne il comportamento e condurre esercizi di ricerca della forma. Tali modelli in scala spesso utilizzavano calze o collant, o pellicole di sapone, poiché si comportano in modo molto simile ai tessuti strutturali (non possono sopportare il taglio).
Le pellicole di sapone hanno uno stress uniforme in ogni direzione e richiedono un confine chiuso per formarsi. Formano naturalmente una superficie minima, la forma con un’area minima e che incarna l’energia minima. Tuttavia sono molto difficili da misurare. Per un film di grandi dimensioni, il suo peso può influire seriamente sulla sua forma.
Per una membrana con curvatura in due direzioni, l’equazione di base dell’equilibrio è:
- {\ displaystyle w = {\ frac {t_ {1}} {R_ {1}}} + {\ frac {t_ {2}} {R_ {2}}}}
dove:
- R 1 e R 2 sono i principali raggi di curvatura per i film di sapone o le direzioni dell’ordito e della trama per i tessuti
- t 1 e t 2 sono le tensioni nelle direzioni pertinenti
- w è il carico per metro quadrato
Le linee di curvatura principale non hanno torsione e intersecano altre linee di curvatura principale ad angolo retto.
Una geodetica o geodetica linea è solitamente la linea più breve tra due punti sulla superficie. Queste linee vengono tipicamente utilizzate quando si definiscono le linee di cucitura del modello di taglio. Ciò è dovuto alla loro relativa rettilineità dopo che i panni planari sono stati generati, con conseguente minore spreco di tessuto e un più stretto allineamento con l’armatura del tessuto.
In una superficie precompressa ma non caricata w = 0, quindi{\ displaystyle {\ frac {t_ {1}} {R_ {1}}} = – {\ frac {t_ {2}} {R_ {2}}}}.
In un film di sapone le tensioni superficiali sono uniformi in entrambe le direzioni, quindi R 1 = – R 2 .
È ora possibile utilizzare potenti programmi di analisi numerica non lineare (o analisi agli elementi finiti ) per trovare e progettare strutture in tessuto e cavi. I programmi devono consentire grandi deflessioni.
La forma finale, o forma, di una struttura di tessuto dipende da:
- forma, o motivo, del tessuto
- la geometria della struttura portante (come pali, cavi, travi anulari ecc.)
- la pretensione applicata al tessuto o alla sua struttura portante
È importante che la forma finale non consenta il ristagno d’acqua, poiché ciò può deformare la membrana e portare a cedimenti locali o progressivi cedimenti dell’intera struttura.
Il carico di neve può essere un problema serio per la struttura della membrana, poiché la neve spesso non scorre via dalla struttura come l’acqua. Ad esempio, questo ha causato in passato il crollo (temporaneo) dell’Hubert H. Humphrey Metrodome , una struttura gonfiata ad aria a Minneapolis, Minnesota . Alcune strutture soggette a ristagno utilizzano il riscaldamento per sciogliere la neve che si deposita su di esse.
Esistono molte diverse forme doppiamente curve, molte delle quali hanno proprietà matematiche speciali. La forma più semplice con doppia curvatura è la forma a sella, che può essere un paraboloide iperbolico (non tutte le forme a sella sono paraboloidi iperbolici). Questa è una superficie a doppia rigatura ed è spesso utilizzata in entrambe le strutture a guscio leggero (vedi strutture iperboloidi ). Le vere superfici rigate si trovano raramente nelle tensostrutture. Altre forme sono selle anticlastiche , varie forme di tende radiali, coniche e qualsiasi combinazione di esse.
Pretensione
La pretensione è la tensione indotta artificialmente negli elementi strutturali in aggiunta al peso proprio o ai carichi imposti che possono sopportare. Viene utilizzato per garantire che gli elementi strutturali normalmente molto flessibili rimangano rigidi sotto tutti i carichi possibili .
Un esempio quotidiano di pretesa è uno scaffale supportato da fili che vanno dal pavimento al soffitto. I fili tengono i ripiani in posizione perché sono tesi: se i fili fossero allentati il sistema non funzionerebbe.
La pretensione può essere applicata ad una membrana allungandola dai suoi bordi oppure pretensionando i cavi che la sostengono e quindi cambiandone la forma. Il livello di pretensione applicato determina la forma di una struttura a membrana.
Approccio alternativo per la ricerca di moduli
L’approccio alternativo approssimato alla soluzione del problema di individuazione del modulo si basa sul bilancio energetico totale di un sistema rete-nodale. A causa del suo significato fisico, questo approccio è chiamato Stretched Grid Method (SGM) .
Semplice matematica dei cavi
Cavo caricato trasversalmente e uniformemente
Un cavo caricato uniformemente che si estende tra due supporti forma una curva intermedia tra una curva catenaria e una parabola . Si può fare l’ipotesi semplificativa che approssimi un arco circolare (di raggio R ).
Per equilibrio :
Le reazioni orizzontali e verticali:
- {\ displaystyle H = {\ frac {wS ^ {2}} {8d}}}
- {\ displaystyle V = {\ frac {wS} {2}}}
Per geometria :
La lunghezza del cavo:
- {\ displaystyle L = 2R \ arcsin {\ frac {S} {2R}}}
La tensione nel cavo:
- {\ displaystyle T = {\ sqrt {H ^ {2} + V ^ {2}}}}
Per sostituzione:
- {\ displaystyle T = {\ sqrt {\ left ({\ frac {wS ^ {2}} {8d}} \ right) ^ {2} + \ left ({\ frac {wS} {2}} \ right) ^ {2}}}}
La tensione è anche pari a:
- {\ displaystyle T = wR}
L’estensione del cavo quando viene caricato è (dalla legge di Hooke , dove la rigidità assiale, k, è uguale a{\ displaystyle k = {\ frac {EA} {L}}}):
- {\ displaystyle e = {\ frac {TL} {EA}}}
dove E è il modulo di Young del cavo e A è la sua area della sezione trasversale .
Se una pretesa iniziale, {\ displaystyle T_ {0}} viene aggiunto al cavo, la prolunga diventa:
- {\ displaystyle e = L-L_ {0} = {\ frac {L_ {0} (T-T_ {0})} {EA}}}
La combinazione delle equazioni di cui sopra dà:
- {\ displaystyle {\ frac {L_ {0} (T-T_ {0})} {EA}} + L_ {0} = {\ frac {2T \ arcsin \ left ({\ frac {wS} {2T}} \ right)} {w}}}
Tracciando il lato sinistro di questa equazione contro T e tracciando il lato destro sugli stessi assi, anche contro T, l’intersezione darà la tensione di equilibrio effettiva nel cavo per un dato carico w e una data pretensione{\ displaystyle T_ {0}}.
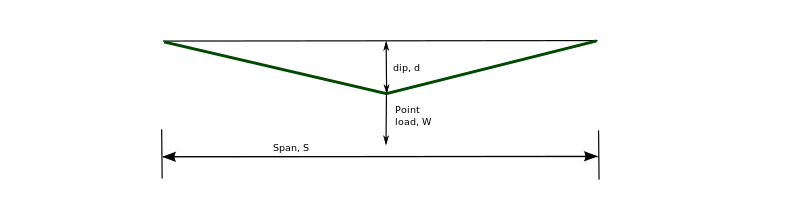
Cavo con carico nel punto centrale
Una soluzione simile a quella sopra può essere derivata dove:
Per equilibrio:
- {\ displaystyle W = {\ frac {4Td} {L}}}
- {\ displaystyle d = {\ frac {WL} {4T}}}
Per geometria:
- {\ displaystyle L = {\ sqrt {S ^ {2} + 4d ^ {2}}} = {\ sqrt {S ^ {2} +4 \ sinistra ({\ frac {WL} {4T}} \ destra) ^ {2}}}}
Questo dà la seguente relazione:
- {\ displaystyle L_ {0} + {\ frac {L_ {0} (T-T_ {0})} {EA}} = {\ sqrt {S ^ {2} +4 \ left ({\ frac {W ( L_ {0} + {\ frac {L_ {0} (T-T_ {0})} {EA}})} {4T}} \ right) ^ {2}}}}
Come prima, tracciare il lato sinistro e il lato destro dell’equazione contro la tensione, T, darà la tensione di equilibrio per una data pretensione{\ displaystyle T_ {0}}e carico, W .
Oscillazioni del cavo in tensione
La frequenza naturale fondamentale , f 1 dei cavi in tensione è data da:
- {\ displaystyle f_ {1} = {\ frac {\ sqrt {\ left ({\ frac {T} {m}} \ right)}} {2L}}}
dove T = tensione in newton , m = massa in chilogrammi e L = lunghezza della campata.
Strutture notevoli
- Rotonda di Shukhov , Russia , 1896
- Canada Place , Vancouver , British Columbia per Expo ’86
- Yoyogi National Gymnasium di Kenzo Tange , Yoyogi Park , Tokyo , Giappone
- Ingalls Rink , Università di Yale di Eero Saarinen
- Khan Shatyry Entertainment Center , Nur-Sultan, Kazakistan
- Tropicana Field , San Pietroburgo , Florida
- Olympiapark , Monaco di Baviera di Frei Otto
- Sidney Myer Music Bowl , Melbourne
- The O 2 (ex Millennium Dome ), Londra di Buro Happold e Richard Rogers Partnership
- Aeroporto internazionale di Denver , Denver
- Dorton Arena , Raleigh
- Georgia Dome , Atlanta , Georgia di Heery e Weidlinger Associates (demolito nel 2017)
- Aeroporto internazionale Grantley Adams , Christ Church , Barbados
- Pengrowth Saddledome , Calgary di Graham McCourt Architects e Jan Bobrowski and Partners
- Scandinavium , Göteborg , Svezia
- Museo della difesa costiera di Hong Kong
- Modernizzazione della stazione ferroviaria centrale , Sofia , Bulgaria
- Redbird Arena , Illinois State University , Normal, Illinois
- Ombrelloni retrattili, Al-Masjid an-Nabawi , Medina, Arabia Saudita
- Torre Killesberg , Stoccarda
Galleria di famose tensostrutture
-
Le strutture tetto tensostrutture di Frei Otto del Olympiapark , Monaco
-
-
La torre di raffreddamento a secco con rete di cavi THTR-300 , struttura iperboloide di Schlaich Bergermann & Partner
-
Torre Killesberg, Stoccarda, di Schlaich Bergermann Partner
-
Grandi ombrelloni retrattili davanti alla Sacra Moschea del Profeta a Medina di SL Rasch GmbH Strutture speciali e leggere
-
Rendering diurno al computer del Khan Shatyr Entertainment Center , la tensostruttura più alta del mondo
Numeri di classificazione
L’ istituto delle specifiche di costruzione (CSI) e le specifiche di costruzione Canada (CSC), edizione MasterFormat 2018, divisione 05 e 13:
- 05 16 00 – Cablaggio strutturale
- 05 19 00 – Assiemi di tiranti e tralicci per cavi
- 13 31 00 – Strutture in tessuto
- 13 31 23 – Strutture in tessuto in tensione
- 13 31 33 – Strutture in tessuto incorniciate
CSI / CSC MasterFormat edizione 1995:
- 13120 – Strutture supportate da cavi
- 13120 – Strutture in tessuto
link
- Buckminster Fuller
- Curvatura gaussiana
- Cupola geodetica
- Geodetiche
- Struttura iperboloide
- Kārlis Johansons
- Kenneth Snelson
- Ponte sospeso
- Tensairity
- Tensegrità
- Fune
Riferimenti
https://www.army-technology.com/contractors/field/sprung-structures2/
Se hai problemi per affrontare i punti suindicati, e vuoi ottimizzare i tempi, potresti valutare la possibilità di frequentare un corso per la preparazione dell'esame di stato di architetto o singole lezioni su ogni argomento legato alla professione di Architetto / Pianificatore Territoriale e/o alla prova d’esame.
________________________________________________________________________ _________________________________________________________________________Pubblicazione gratuita di libera circolazione. Gli Autori non sono soggetti a compensi per le loro opere. Se per errore qualche testo o immagine fosse pubblicato in via inappropriata chiediamo agli Autori di segnalarci il fatto è provvederemo alla sua cancellazione dal sito